9036. Комбинации
игральных костей
Подсчитайте
количество способов, которыми можно получить сумму n, бросая игральный кубик один или несколько раз. Каждый бросок
дает результат между 1 и 6.
Например
при n = 3
имеется 4 способа:
·
1 + 1 + 1
·
1 + 2
·
2 + 1
·
3
Вход. Одно целое число n (1 ≤ n ≤ 106).
Выход. Выведите количество способов
по модулю 109 + 7.
|
Пример
входа |
Пример
выхода |
|
3 |
4 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть f(n) – количество способов, которыми можно получить сумму n. Пусть при последнем броске выпало
число k (1 ≤ k ≤ 6). Тогда
всеми бросками кроме последнего следует получить число n – k, что
можно совершить f(n – k) способами. Таким образом имеем:
f(n) = f(n – 1) + f(n – 2) + f(n – 3) + f(n – 4) + f(n – 5) + f(n – 6)
Сумму n = 1 можно получить только одним способом, бросив кубик один
раз и получив на нем единицу, поэтому f(1) = 1.
Сумму n = 2 можно получить
двумя способами: 1 + 1 и 2, поэтому f(2) = 2.
Пусть n = 3. Можно:
·
одним броском получить 3;
·
последним броском получить 2 и
остальными бросками получить 1, что можно совершить f(1) = 1 способом;
·
последним броском получить 1 и
остальными бросками получить 2, что можно совершить f(2) = 2 способами;
Таким образом f(3) = 1 + f(1) + f(2) = 1 + 1 + 2 = 4.
Аналогично для n ≤ 6 имеем: f(n) = 1 + f(1) + f(2) + … + f(n – 1).
Еще раз рассмотрим нашу рекуррентность:
f(n) = f(n – 1) + f(n – 2) + f(n – 3) + f(n – 4) + f(n – 5) + f(n – 6)
Запишем
уравнение для f(n – 1):
f(n – 1) = f(n – 2) + f(n – 3) + f(n – 4) + f(n – 5) + f(n – 6) + f(n – 7)
Из последнего уравнения выразим сумму
f(n – 2) + f(n – 3) + f(n – 4) + f(n – 5) + f(n – 6) = f(n – 1) – f(n – 7)
и подставим в исходную рекуррентность:
f(n) = f(n – 1) + f(n – 1) – f(n – 7) = 2 * f(n – 1) – f(n – 7)
Вычислим
значения функции для n ≤ 6:
f(1) = 1, f(2) = 2, f(3) = 4,
f(4) = 1 + f(1) + f(2) + f(3) = 1 + 1 + 2 + 4
= 8,
f(5) = 1 + f(1) + f(2) + f(3) + f(4) = 1 + 1 + 2 + 4
+ 8 = 16,
f(6) = 1 + f(1) + f(2) + f(3) + f(4) + f(5) = 1 + 1 + 2 + 4
+ 8 + 16 = 32
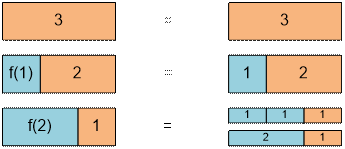
Получили
эквивалентную рекуррентность
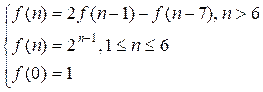
Пример
Вычислим значения функции f(n) для n ≤ 9.

Например,
f(8) = f(7) + f(6) + f(5) + f(4) + f(3) + f(2) = 125,
f(9) = 2 * f(8) – f(2) = 2
* 125 – 2 = 248
Реализация алгоритма
Объявим константы. Объявим массив для вычислений dp.
#include <stdio.h>
#define MAX
1000001
#define MOD
1000000007
long long dp[MAX];
Основная часть программы. Инициализируем значения
от dp[1]
до dp[6].
dp[1] = 1;
dp[2] = dp[1] + 1;
dp[3] = dp[1] + dp[2] + 1;
dp[4] = dp[1] + dp[2] + dp[3] + 1;
dp[5] = dp[1] + dp[2] + dp[3] + dp[4] + 1;
dp[6] = dp[1] + dp[2] + dp[3] + dp[4] + dp[5] + 1;
Читаем входное значение n.
scanf("%d", &n);
Пересчитываем значения dp[7], …, dp[n].
for (i = 7; i <= n; i++)
dp[i] =
(dp[i - 1] + dp[i - 2] + dp[i - 3] + dp[i - 4] + dp[i - 5] + dp[i - 6]) % MOD;
Выводим ответ.
printf("%lld\n",
dp[n]);
Реализация алгоритма –
упрощенная
рекуррентность
#include <stdio.h>
#define MAX 1000001
#define MOD 1000000007
int i, n;
long long dp[MAX];
int main(void)
{
dp[0] =
1;
for (i = 1; i <= 6; i++)
dp[i] =
1 << (i - 1);
scanf("%d", &n);
for (i = 7; i <= n; i++)
dp[i] =
(2 * dp[i - 1] - dp[i - 7] + MOD) % MOD;
printf("%lld\n", dp[n]);
return 0;
}
Java реализация
import java.util.*;
class Main
{
static long dp[] = new long[1000001];
static long MOD = 1000000007;
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
dp[0] = 1;
for (int i = 1; i <= 6; i++)
dp[i] = 1 << (i - 1);
int n = con.nextInt();
for (int i = 7; i <= n; i++)
dp[i] = (2 * dp[i - 1] - dp[i - 7] + MOD) % MOD;
System.out.println(dp[n]);
con.close();
}
}